Moving Beyond the Relative Viscosity Curve — Determining Optimum Plastic Flow Rates: Part 1
Should injection molders consider using a range of plastic flow rates, versus the selection of one plastic flow rate from the relative viscosity curve?
I have been asked countless times how to determine or “know” the optimum plastic flow rate for an injection molding process. Ultimately, it is a subjective question because there are many variables — and some unknowns — which make it hard to state an answer with a high probability.
A typical response is: Fill the mold as “quickly as possible” within the capabilities of the machine while minimizing part defects and avoiding becoming pressure limited. That response, in turn, prompts a host of additional questions such as — how “fast is fast”; how do I know which machines, and therefore press size and capability, my plant will utilize for the job; what, if any, defects are acceptable; what are my KPIs; and, in the event that a mold-filling analysis was conducted, was the plastic flow rate chosen with any rationale or was it simply a guess?
In this instance, it is common for injection molders that apply scientific injection molding principles to generate a viscosity curve — alternatively referred to as relative viscosity, effective viscosity or in-mold rheology curves. This exercise is performed to obtain a range of plastic flow rates based on the shape of the relative viscosity curve and then selecting a specific plastic flow rate to use during the injection phase of the process.
While this method is simple and widely accepted, it does not adequately address the overall impact on processing, and the possibility that specifically selecting one plastic flow rate can be optimized beyond the relative or effective viscosity curve. Furthermore, this method can exclude a range of plastic flow rates from further examination while conducting other scientific injection molding experiments or perhaps a design of experiments (DOE).
Flow Rate’s Influence
Plastic flow rate is the rate at which plastic is displaced from the machine barrel into the injection mold. It is an incredibly important parameter because it directly affects so many different aspects of the process. These aspects include the amount of molecular orientation developed during the injection phase; the decrease in viscosity as the plastic flow rate increases, reflecting the non-Newtonian fluid behavior of thermoplastics; and the generation of shear heat. Shear heat, in turn, impacts the gate-seal time and the amount of thermal energy that must be removed by the mold’s cooling system — which affects the overall cycle time. Also impacted by plastic flow rate: pressure drop through the mold cavity and the ability to adequately pack the injection molded part, as well as the final anisotropic properties, such as part shrinkage variations in the parallel and transverse directions.
A “fast” plastic flow rate is ideal to minimize viscosity variations that will arise from other resin-related factors such as differences in moisture content; the use of regrind; and lot-to-lot disparities in virgin materials. A faster flow rate means the magnitude of these viscosity variations is minimized, and their overall impact on the processing parameters is reduced.
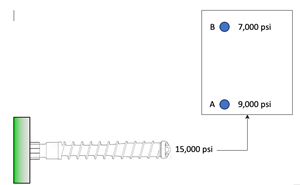
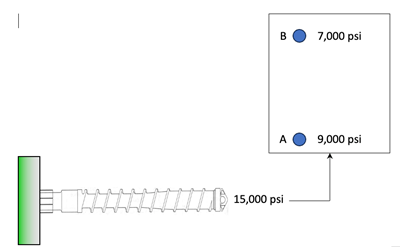
For example, assume that the melt viscosity is 6,000 psi · second and 2,000 psi · second based on two available plastic flow rates. Assume that the viscosity shifts by 5-10% during a production run due to varying moisture content and a change in the material lot. Obviously, a 5-10% change applied to 6,000 psi · second versus 2,000 psi · second makes for a big difference. Think about it this way: Would you rather have 10% of your boss’s bank account or 10% of Elon Musk’s bank account. Both are 10%, but which one puts more money in your pocket?

Fig 1 — Graph of machine hydraulic pressure observed during the injection and packing phases. Source: Umberto Catignani
The relative viscosity curve is generated by sampling the mold at varying plastic flow rates and documenting the machine fill time and peak injection pressure based on the curve shown in Figure 1.
Thereafter, calculating the relative viscosity and shear rate can be done using Equations 1 and 2 and generating a graph of relative viscosity versus shear rate as shown in Figure 2.

Where hr is the relative viscosity, RI is the machine intensification ratio, PPlastic is the plastic pressure, PHydraulic is the hydraulic pressure and TFill is the machine fill time.
It is typical to generate this data over the slowest possible plastic flow rate, perhaps 0.1 to 0.25 in/sec, up to the maximum machine plastic flow rate available. In graphing this data on a linear scale, it generates a curve with the appearance of minimal changes in viscosity at higher plastic flow or shear rates. In reality, the data should be graphed on a logarithmic scale because it is exponential in nature.
The relative viscosity curve was generated for an 8-cavity cold runner mold using PP and is shown in Figure 2.
Fig 2 — Graph of relative viscosities generated using Equations 1 and 2 and applying plastic flow rates between 0.25 and 11.76 in/sec.
After generating this data, it is common to select a range of plastic flow rates that are on the “flat” end of the graph along the X-axis that appear to show a minimal change in viscosity. Selecting a plastic flow rate between 2.0 to nearly 12.0 in/sec appears to be reasonable as the relative viscosity is nearly unchanged at around 5,000 psi·sec.
Thus, one could postulate that using plastic flow rates of 0.25 and 0.5 in/sec is not reasonable, as the relative viscosity is too great to produce the benefits previously mentioned. Graphing the relative viscosity curve while removing these two lower plastic flow rates is shown in Figure 3. In reviewing this graph, the shape of the curve shifts so that the “flat” part of the curve does not exist or at best is between 6.0 to nearly 12.0 in/sec.
Fig 3 — Graph of relative viscosities over plastic flow rates between 1.0 in/sec and 11.76 in/sec.
Therefore, solely using the shape of this curve to determine a range of plastic flow rates can lead to selecting data that is less than ideal based solely on the plastic flow rates chosen during the experiment. The range of ideal plastic flow rates changes from 2.0 to nearly 12.0 in/sec to 6.0 to nearly 12.0 in/sec by removing undesirable plastic flow rates of 0.25 and 0.5 in/sec.
Figure 4 compares the data from the relative viscosity curve to apparent viscosity data generated from a capillary rheometer at isothermal temperatures of 383°F, 401°F and 419°F on a logarithmic scale.

Fig 4 — Graph of relative viscosities as illustrated in Figure 2, and apparent viscosities generated with a capillary rheometer.
When comparing the data from Figure 4, the relative viscosity is off by a factor nearly 1 × 105 (100,000), and the shear rate is approximately off by a factor of 1 × 106 (1,000,000).
Using Equation 1 does not represent a melt viscosity. Calculating the area under the curve during the injection phase would be more useful but it is still not the melt viscosity of the material. Furthermore, we are calculating the area of a rectangle, noted by the green dotted lines in Figure 1 that calculate the area existing between the maximum observed hydraulic pressure and machine fill time.
For a viscosity to be relative, it would be ideal to apply a shift factor to produce a melt viscosity that correlates a plastic flow rate from the relative viscosity curve to the apparent viscosity. In other words, applying a shift factor to state that a specific machine plastic flow rate of 7.0 in/sec generates a shear rate that is perhaps 1,000 reciprocal seconds with an apparent viscosity of 1,500 psi · sec. It may be possible to generate a shift factor, but keep in mind this experiment is meant to be conducted in a production environment where time is of the essence.
Mold filling analysis, such as Autodesk’s Moldflow Insight (AMI), calculates the melt viscosity in a mold cavity using the Cross/Williams-Landel-Ferry (WLF) viscosity model for its simulations. This model describes the temperature, shear rate and pressure dependency of the melt viscosity for thermoplastic materials. The viscosity model is expressed as:

Where h is the melt viscosity; h0 is the zero shear viscosity or the “Newtonian limit” where viscosity approaches a constant at very low shear rates; γ is the shear rate; τ* is the critical stress level at the transition to shear thinning, which is determined by curve fitting; and n is the power law index in the high shear rate regime which is also determined by curve fitting. The zero-shear viscosity is expressed by:

Where T is the temperature; A2= A2+D3P, where Tθ is the glass transition temperature given by D2+D3P; and P is the pressure. A1, A2, D1, D2 and D3 are model constants, while D3 describes the pressure dependence of the viscosity.
In closing, we can conduct multiple experiments to generate data that will provide greater insight while using a range of plastic flow rates, versus the selection of one plastic flow rate from the relative viscosity curve.
This analysis leads to selecting a range of plastic flow rates based on additional experiments and thus using plastic flow rates as a parameter for DOE. Potential benefits include: reducing cycle times and scrap rates while further understanding the capability, repeatability and reproducibility of the injection molding machine; providing greater insight into data obtained by additional scientific injection molding experiments; and the ability to document the injection molding processing parameters such that they can be transferred to a second machine, duplicating the four primary plastic conditions with a higher confidence level.
In the next several articles, we will compare the results of the relative viscosity curve to other experiments using a range of plastic flow rates to gather additional insights for further optimization of the injection molding process.
ABOUT THE AUTHOR: Umberto Catignani is president of ., a consulting firm that has more than 125 years of combined experience in scientific injection molding, training, material selection, part and mold design review, in-mold instrumentation, project management and equipment selection. Catignani is a past president of the Southern Section of SPE and has more than 29 years of hands-on injection molding experience. He has certified and trained hundreds of plastic professionals in the industry and has served as an expert witness. Past employers include IBM, General Motors, Delphi Automotive and Husky Injection Molding Systems. Catignani earned a master’s degree in polymer engineering from The University of Akron and a bachelor’s degree in materials engineering from the University of Cincinnati. Contact: 404-849-6714; umberto@orbitalplastics.com
Related Content
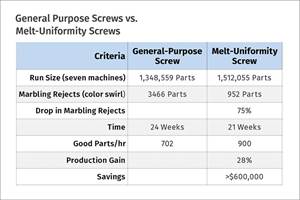
Improve Production Rates Via Screw Design — Barrier vs. General Purpose vs. Melt Uniformity
I’m looking for a few good molders to help trial a new screw design, and share data and results for a future article to prove the benefits of a melt uniformity screw.
Read MoreHome In on These Six Variables to Monitor Molding
There are hundreds of variables in molding, but focusing on these six will help you make consistent parts.
Read MoreUnderstanding the Effect of Pressure Losses on Injection Molded Parts
The compressibility of plastics as a class of materials means the pressure punched into the machine control and the pressure the melt experiences at the end of fill within the mold will be very different. What does this difference mean for process consistency and part quality?
Read MoreA Systematic Approach to Process Development
The path to a no-baby-sitting injection molding process is paved with data and can be found by following certain steps.
Read MoreRead Next
Understanding the Effect of Pressure Losses on Injection Molded Parts
The compressibility of plastics as a class of materials means the pressure punched into the machine control and the pressure the melt experiences at the end of fill within the mold will be very different. What does this difference mean for process consistency and part quality?
Read MoreImportant Factors and Approaches to Estimating Residence Time in Injection Molding
Residence time can have a dramatic impact on part quality and production efficiency but determining its value can be tricky. Use these methods and formulas to accurately measure residence time and enable it to inform everything from scheduling jobs to optimizing a process.
Read MoreUnderstanding the Effect of Polymer Viscosity on Melt Temperature
Every processor should get hold of the viscosity curves for the polymers they use or contemplate using in their operations, and learn how to read them.
Read More