����ý

In part one, the importance of understanding a material’s bulk density was discussed. In part two, we’ll address two other densities that are equally important to injection molders: solid density, sometimes simply referred to as density, and melt density.

Solid density is the most commonly used number by designers and processors. It is defined as the weight per unit volume for a given material. For example, if you molded a 1-cm cube using a generic unfilled polypropylene (PP), then the weight of the cube will be the density of the PP. The volume of the cube is 1 cubic centimeter (cm³), and if the weight is 0.91 gram, then the weight per unit volume (or density) will be 0.91 g/cm³. The figure 0.91 is in fact the widely used density for PP. 

Featured Content

A Simpler Way to Calculate Shot Size vs. Barrel Capacity READ MORE

Automatic Conveying with AI Optimization READ MORE

3 Ways to Reduce Costs in Your Plastics Process Cooling Systems READ MORE

Because specific gravity is sometimes confused with density, we will have a quick explanation here. The density of water is 1 g/cm³, meaning if we could mold a cube of water with dimensions of 1 × 1 × 1 cm, it would weigh 1.00 gram. Specific gravity is defined as the ratio of the density of the material under consideration compared to the density of water. Considering PP from above, its specific gravity would be 0.91/1.00 which equals 0.91 (because this is a ratio there are no units). Numerically, the numbers for density, as well as specific gravity, are the same and that’s the reason why the two terms are confusing and often used interchangeably. However, each has its own place, and their significance must be understood. Material datasheets provided by resin manufacturers are the source of the solid density or specific gravity values.

Why Part Weight Matters

The weight of a molded part is required for two main reasons. First, to determine the amount of raw material that will be needed to mold a given quantity of parts; and second, to find a suitable machine to mold the parts. When a designer first designs a part, it is only a CAD model — there are no physical components. To determine what the part will weigh, the designer will need to multiply the volume of the part with the density of the material from which it will be molded. The CAD model will provide the volume of the part.

If the material changes, the density will change and therefore the part weight changes. Production molds can have multiple cavities with multiple cold runners. In this case, the weight of the runners also needs to be estimated using the same formula and then added to the part weight. This combined weight of the parts and runners is called the shot weight. To calculate the amount of material required for production, the shot weight is multiplied by the number of required cycles. The cost of the material is then calculated based on the amount of required material.

To determine the part’s weight, the designer will need to multiply the volume of the part with the density of the material from which it will be molded.

To establish a robust process, it is important to have a correctly sized barrel. The machine manufacturer usually publishes the maximum machine barrel capacity in terms of weight. The ratio of the weight of the injected shot to the barrel capacity should not be too small or too big as this leads to inconsistency in product quality and process control. The preferred ratio of the shot weight to the max barrel capacity is between 20% and 80%. For example, if the maximum barrel capacity is 100 g, then the shot weight should not be less than 20 grams or more than 80 grams. (There can be some exceptions to these percentages, but that discussion is beyond the scope of this article).

If the published barrel capacity is given in weight, then that weight is always given in terms of the weight of polystyrene (PS). For example, if the published weight is 100 grams, that means the maximum amount of PS that the barrel will hold is 100 grams or, in other words, the largest shot that can be molded will be 100 grams of PS. This means that the maximum volume of the barrel, which is in the form of a cylinder, is fixed and holds 100 grams of PS.

The density of PS is 1.06 g/cm³. If we were to replace the PS with a material with a higher density, then the total shot weight will increase. For example, if we replace the PS with a glass-filled polyester (PBT) that has a density of 1.53, then the barrel will now hold 144 grams of the PBT. The barrel’s volume stays the same, but because the density of the material is higher, the total weight is also higher. Figure 1 illustrates this concept using a bucket filled with different materials. Figure 2 shows the concept with the injection molding barrel and the calculated values for different materials. To convert the barrel capacity from PS to the material being molded, use the following formula:

The percentage usage of the barrel should be based on the barrel capacity and considering the material that is being molded. Knowledge about and the value of the density is therefore critical for such calculations.

It is not uncommon that the material being used to mold a product must change. This could be the result of the first-choice material not performing as intended out in the field, forcing a replacement with a material that meets the customer’s requirements. A part that is breaking may need a glass-reinforced resin, for instance. In a recent project I worked on, a material had to be replaced because the original resin was leaving a residue in the mold cavities and causing cosmetic defects. Material replacement could also be due to financial considerations if a material supplier increases the resin’s cost and a cheaper replacement must be found.

While searching for alternative resins, it is critical that manufacturers don’t focus only on the resin’s price per pound. A cheaper resin could have a higher density, which requires more resin for the job and drives up the cost per part. Calculate the weight of the shot based on the density of the material being considered and then calculate the impact on the cost. The new and old costs should be compared before any decision is made.

Calculating Melt Density

The third type of density is called the melt density and it is a critical specification processors need to know. When the plastic is in the solid form, its density is known as the solid density or simply density. When the processor feeds the resin into the molding machine, the plastic melts and the molecules move away from each other, thereby lowering the material’s density. The density of the molten material is known as the melt density. Pressure-volume-temperature (PVT) diagrams, such as the one shown in Figure 3, are often used to determine a material’s melt density.

Melt density is mainly used to calculate the actual maximum shot capacity of the machine rather than rely upon the machine manufacturer’s number. Why? It’s not that manufacturers provide incorrect numbers, but rather that the number they provide is just a close estimate. As seen from the PVT diagram, melt density is a function of temperature and pressure. Considering the molten plastic in the barrel, the temperature is the product of the barrel settings and shear from the screw rotation speed, while the pressure results from the back pressure during the screw recovery process.  

In recent years, in addition to the maximum shot weight in terms of PS, machine manufacturers have started publishing the maximum machine capacities in terms of volume, because volume is independent of the material or its density. It is now up to the processor to figure out the maximum shot weight based on the material being molded. In this case, molders must use the melt density to accurately calculate the shot capacity. Using solid density will give a number that will be higher and therefore incorrect. Processors tend to multiply the solid density figure by a factor of between 0.70 and 0.80 to estimate the melt density.

The ratio of the weight of the injected shot to the barrel capacity should not be too small or too big as this causes issues with inconsistency in product quality and process control.

Set aside all this to say, calculating melt density is surprisingly easy! There is a much easier method to obtain the exact number. The only requirement here is that the molder should have molded the material before. Even a similar grade of the material is good enough for our calculation.

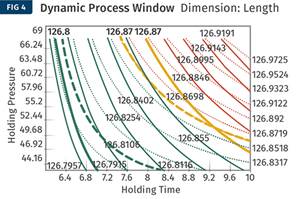
Given that the formula for calculating weight is — Weight = Volume × Density — the calculation for obtaining density is: Density = Weight/Volume. In a known molding process, the weight will be equal to the shot weight, which again, is the weight of all the parts and the runners. The volume will be the total volume displaced by the screw, which will be from the shot size to the cushion value (see Figure 4 for an example). Here, the melt temperature is 380°F and the back pressure is 500 psi, with a screw diameter of 35 mm. The set shot size is 104.6 mm and the cushion value is 6.6 mm. By using the formula for determining the volume of a cylinder — 0.785 × D × D × L — (where D is the diameter of the screw and L is the total distance traveled), we calculate the volume injected to be 94.28 cm³ (note the conversion of mm to cm.) This volume molded a shot weight of 63.17 grams. Using the formula for density, the calculated melt density is 0.67 g/cm³.  

The melt density here is 70% of the solid density or at a factor of 0.70 of the value of 0.95 g/cm³. It is important to remember that this was at a melt temperature of 380°F and a back pressure of 500 psi. The commonly used factor of 0.70 to 0.80 is a good estimate, but performing this calculation gives us much more accurate values.

This two-part article covered the basics of the three types of densities in injection molding. It is always a good practice to document the three types of densities for all the materials used in a molding operation. For melt density, molders could even go one step further and generate an empirical formula or a graph to calculate the value based on melt temperature and back pressure.

ABOUT THE AUTHOR: Suhas Kulkarni is the founder and president of , San Diego, an injection molding service-oriented firm focusing on scientific molding. FimmTech has developed several custom tools that help molders develop robust processes, and its seminars have trained hundreds of individuals. Kulkarni is an author of the bestselling book, “Robust Process Development and Scientific Molding,” the third edition of which was published by . Contact: 760-525–9053; suhas@fimmtech.com; .